This is the archived website of SI 335 from the Spring 2013 semester. Feel free to browse around; you may also find more recent offerings at my teaching page.
Readings:
- DPV, Chapter 1, everything except 1.5.
- CLRS, Chapter 31: Everything except 31.4 and 31.5, and just skim 31.9. Also Chapter 17, intro and 17.1.
Algorithms: in python
- Slides: note-taking version
- These notes: printable version
Beginning of Class 11
1 Why Number Theory?
Number theory is the branch of mathematics that studies integers and the structures they form with different operations like multiplication and "mod". (And yes, there is a whole lot to study under that heading. Think whole conferences, book series, careers...)
But this is not a math class. So you might be wondering why we would study number-theoretic computation in an algorithms class. Well, several reasons:
- The very first true algorithms were number-theoretic algorithms, so the history of "algorithm" and thus computer science is tied up in them.
- Some interesting analysis comes up when we examine the running times of some of these algorithms.
- Modern cryptography is built around this stuff! This should be enough motivation, in fact. You'll actually implement the RSA algorithm, which is the foundation of many encrypted transactions on, for instance, the internet.
- Several other CS topics, like hashing, rely on understanding this stuff.
- You learned in Architecture that your entire computer is really just made up of integers (of a certain bit-length). So somehow, at the core, all computer algorithms are number-theoretic algorithms!
2 The size of an integer
In algorithms that work with arrays, we used the size of the array as a reasonable measure of difficulty. What measure should we use for operations whose input is integers? Let's look at an example problem to help answer this.
2.1 Factorization
What did it mean to say that number theory studies the "structures" that the integers form under multiplication and mod? Well, for multiplication, this typically means looking at the factorization of an integer.
Recall that an integer is prime if the only integers that divide it evenly are 1 and itself. Any integer that is not prime is composite and can be written (uniquely) as a product of its prime factors — this is called its (prime) factorization.
To discover the prime factorization of an integer \(n\), it suffices to find just a single prime factor \(p\) of \(n\). Then, if we want the complete factorization, we could recursively find the factors of \(n/p\). For example, if to factor the integer \(n=45\), we might first find that 3 divides 45, then (with a recursive call) factor \(n/3=15\) into 3 times 5 for the complete prime factorization \(45 = 3\times 3\times 5\).
2.2 Algorithm for Factorization
The most obvious way to find a prime factor of a number \(n\) is to try dividing it by every integer from 2 up to \(n-1\). If none of those divide n, then n must be prime.
But wait — there's an easy improvement to this. Say n is not prime, so it has two factors a and b both greater than 1, \(n=ab\). At least one of these factors must be less than \(\sqrt{n}\). (Otherwise their product would be strictly greater than n.) So we really only need to check for divisors from 2 up to \(\lfloor\sqrt{n}\rfloor\). If there aren't any divisors in this range, then there aren't any at all.
leastPrimeFactor
Input: Positive integer
nOutput: The smallest prime
pthat dividesndef leastPrimeFactor(n): i = 2 while i * i <= n: if n % i == 0: return i i = i + 1 # If we get here, n must be a prime number itself. return n
Now clearly the running time of this algorithm is determined just by the maximum number of iterations of the while loop. The worst case is when \(n\) is actually prime (so the loop never returns on line 3), and the total cost is \(\Theta(\sqrt{n})\).
This seems pretty fast. Sub-linear time, right? Wrong! The issue is with the measure of difficulty. Here the integer n is the actual input integer, but we usually want to measure the cost of algorithms in terms of the size of the input.
By size here we mean how much actual computer memory this object (an integer) takes up. Normally when we talk about integers we really mean ints, which are bounded by \(2^{32}\). These are called single-precision integers. When we start working with really really big numbers, we sometimes need multiple words of memory to store them. These are called multi-precision integers.
So the size of an integer is just 1, if it's single-precision, and otherwise it's proportional to the number of bits in the binary representation of that integer, which equals \(\lceil \lg (n+1) \rceil\). So the real measure of difficulty should look more like \(\log n\). This will make the cost of this algorithm look very different!
For what follows, we'll define s as the size of n in machine words. So \(s \in \Theta(\log n)\). The cost of the above algorithm in terms of s is now really really bad: \(\Theta(2^{s/2})\).
Beginning of Class 12
2.3 Polynomial Time
The notion of polynomial time is really important in the history of algorithm development and analysis. We say that an algorithm is polynomial time if its cost is \(O(n^c)\) for some constant c. Of course c could be really really big, but as long as it doesn't change depending on the input, this is considered polynomial time.
Why do we care about polynomial-time? It relates to a "thesis", which is to say, an unproven assertion about what kind of algorithms will be ever be feasible for computation. Think of this as the algorithms analogue of Moore's law for hardware.
Cobham-Edmonds Thesis
An algorithm for a computational problem can be feasibly solved on a computer only if it is polynomial time.
Now let's see how this relates to factorization. The "true" cost, in terms of the input size, we have seen to be \(\Theta(2^{s/2})\). This is definitely not polynomial time. So if we believe the Cobham-Edmonds Thesis, than this algorithm will never be feasible for large inputs.
Of course better, faster factorization algorithms have been developed that the one above. But even the best (based on something called the general number field sieve) are not polynomial time. So it appears that, although it looked at first that our algorithm was fast, factorization is actually a hard problem, one that can't be solved efficiently by computers for sufficiently large inputs.
3 Modular Arithmetic
3.1 Grade school division and the definition of "mod"
Suppose a is a non-negative integer, and m is a positive integer. To both mathematicians and grade school students dividing a by m means there are two numbers, a quotient q and a remainder r, such that \(a = q m + r\), where \(0 \le r \lt m\). In fact, q and r are unique. The definition of "\(a \bmod m\)" is that it equals the remainder r.
As we will see, this operation of "mod" actually defines a separate world of computation, for each different denominator (or "modulus") m. By this I mean, if we do all of our normal arithmetic operations "mod m", then some interesting patterns emerge.
3.2 Modular addition
Let's look at the "world" that gets created with the operation of addition and the modulus \(m=15\). The following table shows \(a+b\bmod 15\) for every \(a,b\) from 0 up to 14:

Addition mod 15
See how regular the structure is? But how do I know that this is really the whole "world" of mod-15 addition? What if we added up bigger numbers and took the sum mod 15? It turns out, that is exactly the same as if we took the big integers mod 15 first, then took their sum mod 15. Since every "mod 15" gives an integer in the range above (0 to 14), that's really all there is!
In case that last paragraph lost you, here's a formal restatement:
Theorem
For any integers \(a,b,m\) with \(m > 0\),
\((a + b) \bmod m = (a \bmod m) + (b \bmod m) \bmod m\)
To prove facts like this one, all it takes is to write out the division-with-remainder of the original numbers by m, and then see what happens. Here, say \(a=qm+r\), \(b=sm+t\), and \(r+s=um+v\). Then \(a+b\) equals \((p+q)m+(r+s)\), which equals \((p+q+u)m + v\). So \((a+b)\bmod m\) equals \(v\), which is the same as \((r+s)\bmod m\). Q.E.D.
This fact is really important for computation. For example, let's say we wanted to add up a million integers, and then take the sum mod 15. To do this quickly, we could add the numbers in one at a time, taking the sum so far mod 15 at every step along the way. We would get the same answer, but wouldn't ever have to add any numbers larger than 14. So we could actually do it in our heads (although, for a million numbers, it might take a while).
Now let's think about subtraction. First, subtraction is just like addition, with a negative number. So \(24 - 11\) is really just \(24 + (-11)\). And a negative number is just something that adds with the original number to zero. For example, -11 is just the number that, when added to 11, gives us 0.
No surprises so far. But let's try to apply these concepts to the "mod 15" world. Look back at the table and you'll see that a single 0 appears in every row and column. This corresponds to the additive inverse mod 15! In fact, we can say exactly what it is: For any \(1\leq a < m\), \(-a\bmod m\) is equal to \(m-a\). This makes sense, because \(a+(m-a)=m\), which is always equal to 0 mod m.
So this means that we can write things like \(4 - 10 \bmod 15\), and it makes sense. And since subtraction is just a short-hand for addition, the same rule as above applies: we can take \(-10\bmod 15\) and add it to 4, or we can subtract \(4-10=-6\) and take that mod 15 — either way, it's always going to come out the same.
3.3 Modular Multiplication
Now let's delve into the world of multiplication mod 15:

Multiplication mod 15
Ooh, so much more complicated than addition! Let's see if we can't make some sense of it. The first thing we need is another theorem analogous to the one above on taking "mod"s before or after addition:
Theorem
For any integers \(a,b,m\) with \(m > 0\),
\((ab) \bmod m = (a \bmod m)(b \bmod m) \bmod m\)
The proof is pretty similar: Write \(a = qm+r\), \(b=sm+t\) and \(rt=um+v\). Then
\(ab = (qm+r)(sm+t) = qsm^2 + qtm + rsm + rt = (qsm + qt + rs)m + rt\) \(= (qsm+qt+rs+u)m + v\).
So multiplying a and b, then taking the answer mod m, is the same as taking each of a and b mod m, then multiplying and doing one last mod m to get the same result, every time. Q.E.D.
Again, you should recognize the importance to computation: for example, try computing \((418942\times 423809) \bmod 3\) in your head. Can't do it? Well, if you remember a trick from grade school, you might be able to figure out that 418942 mod 3 is 1, and 423809 mod 3 is 2, so the product is just 2 mod 3!
Beginning of Class 13
3.4 Modular Division?
The game with division is similar to subtraction, at least at first. We need to recognize that division is really just multiplication with an inverse. So \(a/b\) just means \(a\times b^{-1}\), where \(b^{-1}\) is defined as the number which, when multiplied by b, gives 1.
So look up at the table for multiplication mod 15 to see if we can find some inverses. We're looking for a "1" in every row and column...
Some numbers have a multiplicative inverse. Like \(13\times 7 \mod 15= 91\bmod 15 = 1\), so \(13^{-1} \bmod 15 = 7\). This means we can do division by 13 (or by 7) in the "mod-15 world".
But some of the numbers don't have any inverse mod 15. Specifically, 0, 3, 5, 6, 9, 10, and 12 have no "1" in their rows or columns, hence no multiplicative inverse. If you think for a minute, you might realize that these are exactly the numbers that share a common factor with 15. To see why this happens, take any integers a, b, and m, and say a and m they are both divisible by another integer c. Then if we have \(ab=qm+r\), then because a and \(qm\) are divisible by c, r must be divisible by c too, no matter what b is. But if \(c>1\) (i.e., if it's an actual common factor), then this means there is no number which multiplies with a to give 1 mod m.
Now that we understand what makes numbers have no inverses mod m, what kinds of m will give the multiplicative world lots of inverses? The ones that don't have any factors - the primes! For example, here is a table of multiplication mod 13:

Multiplication mod 13
Now we see that every row and column (except 0) has exactly one "1" in it, corresponding to the multiplicative inverses mod 13. This is happens precisely because 13 is a prime number, with no factors other than 1 and 13.
Incidentally, this "how many multiplicative inverses are there mod m" question is so important that mathematicians gave it a special name. Actually, it's a function that has a name: Euler's totient function, usually denoted \(\varphi(m)\). We know already that \(\varphi(m)=m-1\) if and only if \(m\) is a prime, and otherwise it's smaller than \(m-1\). How much smaller is a question far beyond this course, but we know at least one value: \(\varphi(15)=8\). Later we'll see how to generalize this just a bit.
3.5 Modular Exponentiation
Now once we have multiplication we naturally want to compute powers! Actually much of modern cryptography involves computing \(M^e \bmod m\) where M, e, and m are all really big numbers. Again, using the facts we know about modular arithmetic will be greatly helpful for computing these quickly.
For example, could you compute \(3^{2013} \bmod 5\) in your head? Obviously we're not going to compute \(3^{2013}\) first — that would be a really huge number!
A slightly better way would be to compute \(3\times 3\times\cdots\times 3\) 2013 times, taking the result mod 5 after each multiplication. This would take 2013 multiplications, but each of them would be really easy, so we could probably do it.
But let's improve this even more. How could we make a divide-and-conquer strategy for integers? Notice that every positive integer e can be written as \(e = 2u + v\), where u is non-negative and v is either 0 or 1. Actually, v is just the last bit of e in binary, and u is all the other binary bits.
Let's see how this helps with \(3^{2013} \bmod 5\). Write \(2013 = 2*1006 + 1\), and then
\(3^{2013}=3^{2*1006+1}=(3^{1006})^2*3\).
So we've reduced to a smaller subproblem, computing \(3^{1006}\), and then a single "square mod 5" and "times 3 mod 5". Continuing this way, we cut our 2013 multiplications down to about 20. This algorithm (I'm not going to write it out) is variously called either "binary powering" or "square-and-multiply". To actually do it, all we need is the binary representation of the exponent — and we probably have this already if we're on a computer! The recursive version is as I've described above, and there is actually a slightly faster iterative version that works starting from the most-significant bit instead... I'll let you figure it out. The cost either is \(\Theta(\log n)\) multiplications mod \(m\).
Could we compute \(3^{2013}\) even faster than that? Actually, yes! It's because the modulus 5 is so very small. We know that \(\varphi(5)=4\) (why?). Now there's a magical property that for any positive numbers a and m that don't share any common factors, \(a^{\varphi(m)} \bmod m = 1\). (This property is so special that it has a name: Fermat's Little Theorem.) So any integer less than 5, raised to the 4th power, is equal to 1 mod 5. But 1 raised to any power, mod anything, is still equal to 1. So we have another general property:
\(a^e\bmod m = a^{e\bmod \varphi(m)} \bmod m\).
Since \(2013=503*4+1\), we can write \(3^{2013} \bmod 5 = 3^1\bmod 5 = 3\). This cuts down significantly on the number of multiplications required! (And it's also part of the reason why we always use much much much bigger moduli in cryptography.)
Beginning of Class 14
4 The Euclidean Algorithm
One of the fundamental problems of arithmetic with integers is to find the greatest common divisor of two integers a and b, i.e. the largest integer that evenly divides both numbers. This problem turns out to be far more important that one would ever imagine, being a part of things as diverse as integration, encryption, and even compiler optimization.
This very basic problem inspired what is considered by many to be the first real algorithm: the Euclidean Algorithm. Euclid's name is attached to this algorithm, though he probably did not invent it, because it appears in his famous book The Elements (c. 300 B.C.). So, we're talking about a pretty old algorithm here!
Let u and v be two nonnegative integers: The Euclidean GCD Algorithm is based on the following two observations:
- \(\gcd(a,0) = a\)
- \(\gcd(a,b) = \gcd(b, a \bmod b)\)
How does this turn in to an algorithm for computing GCD's?
GCD (Euclidean Algorithm, recursive version)
Input: Integers
aandbOutput:
g, the gcd ofaandbdef gcd(a, b): if b == 0: return a else: return gcd(b, a % b)
It's harder to analyze, but slightly faster in implementation to write the algorithm iteratively: Although we'll generally use the algorithm above for our analysis, it's often more useful in practice to use the iterative version below:
GCD (Euclidean Algorithm, iterative version)
Input: Integers
aandbOutput:
g, the gcd ofaandbdef gcditer(a, b): while b != 0: (a, b) = (b, a % b) return a
Based on what we've been working on in this class, you should now be clamoring for some analysis of this algorithm. Since it's recursive, we should start by writing a recurrence relation.
- \(T(a,b) = 1\) if \(b=0\)
- \(T(a,b) = D(a,b) + T(b,a \bmod b)\) if \(b > 0\)
Here we used \(D(a,b)\) to stand for the cost of dividing a by b to get the remainder. If a and b are multiple-precision, and we use the standard algorithm for division with remainder, then this is \(\Theta((\log a)(\log a - \log b))\).
But let's not worry about that for the moment. For now, assume a and b are both single-precision, so that \(D(a,b) \in \Theta(1)\). Then all we really need to analyze is the number of recursive calls it takes to get to the base case.
Now we need to know how large \(a\bmod b\) can be in the worst case. All we can really say is that \(a\bmod b \leq b-1\), from the definition of division with remainder. Notice that this bound is only based on b and not a. So the last simplification we'll make to the recurrence above is to drop the first parameter of \(T(a,b)\) and just analyze with the cost based on the value of the second input, \(T(b)\). This leaves us with:
- \(T(b) = 1\) if \(b=0\)
- \(T(b) \leq 1 + T(b-1)\) if \(b>0\)
By now you should be able to solve this recurrence with the tools that we have to get \(T(b) \in O(b)\). Is this good or not? Remember that b is the actual input integer, with size \(\Theta(\log b)\). So this analysis tells us that the Euclidean algorithm is exponential-time, and therefore infeasible!
Actually, a more refined analysis is possible, but we have to look down two levels into the recursive structure. If a and b are the original inputs, then write
- \(a = q_1 b + r\)
- \(b = q_2 r + s\)
These correspond to the first two recursive steps in the algorithm. The integer s will be the second argument in the second recursive call, so that \(T(b) \leq 2 + T(s)\) if \(b\) is sufficiently large. But how big will \(s\) be? There are two cases to consider:
- Case 1: \(r \gt b/2\). Then \(q_2=1\), since \(2r>b\). This means that \(s = b-r < b/2\).
- Case 2: \(r \le b/2\). Because \(s \lt r\), this means that \(s\lt b/2\).
In both cases, we see that \(s \lt \frac{b}{2}\), giving the relationship \(T(b) \leq 2 + T(\frac{b}{2})\) when \(b > 0\). Now you should recognize this as being essentially the same as the recursion for binary search, which we know will give \(T(b) \in O(\log b)\). Much better! This is now linear-time in the size of the input.
But is this the best we can do? It's still just a big-O bound. Maybe by looking down three levels into the recursion we could get an even smaller bound?
Actually, no. Turns out, this is really the worst-case cost. To get a matching lower bound, we need to find a family of examples that has the worst-case cost. It just so happens that the worst-case for the Euclidean algorithm is the Fibonacci numbers, which is a very famous sequence defined by
- \(f_0 = 0\)
- \(f_1 = 1\)
- \(f_n = f_{n-1} + f_{n-2}\) if \(n\ge 2\)
It should shock you that these give the worst case for the GCD algorithm. Why? Where did they come from? Well, Fibonacci numbers show up in nature all over the place, and this is just another example. Anyway, because we're just getting a lower bound here (we already have the upper bound analysis), you don't even have to believe me that these give the worst case.
So let's analyze the cost of computing \(\gcd(f_n, f_{n-1})\). Notice that, for any \(n\), \(f_n \mod f_{n-1} = f_{n-2}\). Therefore the sequence of b's in the recursive calls will just be all the Fibonacci numbers \(f_{n-2}, f_{n-3}, \ldots f_0\), the last of which is 0 and causes the algorithm to terminate. So the total cost of \(\gcd(f_n, f_{n-1})\) is the number of recursive calls, which is \(\Theta(n)\).
To understand what this means, we need an upper bound on the size of \(f_n\). This one's easy since we already have an idea of what we're looking for:
Theorem: \(f_n \lt 2^n\), for any \(n\)
Proof: We will prove the statement by induction on n. There are two base cases. \(f_0 = 0 \lt 1 = 2^0\). And \(f_1 = 1 \lt 2 = 2^1\).
Next we assume the statement is true for all \(n \leq k\). Then \(f_{k+1} = f_{k} + f_{k-1} \lt 2^k + 2^{k-1} < 2*2^k = 2^{k+1}\).
By the (strong) induction, the statement is therefore proven for all \(n\ge 0\).
This allows us to write \(T(2^n) \ge T(f_n) = n\). Substituting \(2^n=b\), we have \(T(b)\in\Omega(\log b)\).
This matches the upper bound from above, so that we can write a big-Theta for the total cost: \(T(b) \in \Theta(\log b)\). Now remember this was only for single-precision inputs. In multiple precision, the size of both operands is important, and the cost is more like \(O((\log a)(\log b)^2)\). This is a little worse, but it's still polynomial-time in the size of the input.
4.1 The extended Euclidean algorithm
Remember the connection between gcd's and modular arithmetic? In the "mod m" world, a number a has a multiplicative inverse if and only if \(\gcd(m,a) = 1\). So the Euclidean algorithm above gives us a way to figure out when numbers have inverses. For example, 12 is not invertible mod 15 because \(\gcd(15,12) = 3\). But 8 does have an inverse mod 15 since \(\gcd(15,8)=1\).
But this still leaves us with the problem of actually finding that inverse! What number can be multiplied with 8 to get 1 mod 15? So far, we know that such a number exists, but our only way to find it is to write out \(8x\bmod 15\) for every possible \(x\) until we find it.
Well, we can do better than that. There's an extended version of the Euclidean algorithm that keeps track of extra information along the way to solve this problem for us. This algorithm computes not just the gcd of its arguments, but also two numbers called the cofactors. Specifically:
XGCD (Extended Euclidean Algorithm)
Input: Integers
aandbOutput: Integers
g,s, andtsuch thatg = GCD(a,b)and \(as + bt = g\).def xgcd(a, b): if b == 0: return (a, 1, 0) else: q, r = divmod(a, b) (g, s0, t0) = xgcd(b, r) return (g, t0, s0 - t0*q)
How can this be used to find multiplicative inverses? Well say m is the modulus, and \(\gcd(m,a) = 1\), so that a has a multiplicative inverse mod m. Then XGCD(m,a) will return the tuple \((1,s,t)\) such that \(1 = sm + ta\). Flipping this around, we get \(ta = (-s)m + 1\), meaning that \(ta \bmod m = 1\). So the last integer returned by the extended Euclidean algorithm is exactly the inverse of a mod m. And the cost is \(\Theta(\log a)\) steps, just like for the regular Euclidean algorithm.
Beginning of Class 15
5 Encryption
Remember that Number Theory is the branch of mathematics that studies the integers. It was long looked at as the most "pure" of mathematical pursuits, in that it would never have practical applicability and thus was only to be studied for its beauty. However, number theory has suddenly become very practical, as it underpins much of the subject of modern cryptography — and cryptography is of immense importance in the ever more connected world in which we live.
At its core, cryptography is all about sending a message in such a way that only the intended recipient can read it. So to even talk about this stuff, we have to say precisely what constitutes "a message". For us, a message will simply be a sequence of non-negative integers. The upper-bound on the size of each number will be \(2^B\), where B is called the "block size" of the encryption scheme. We will consider each of these numbers (or "blocks") as separate encryption problems.
5.1 Conventions for this lecture
For this lecture, we will consider a block-size of 10, so every message consists of 10-bit blocks, i.e. of numbers in the range \([0..2^{10}-1]\). We will agree on the following 5-bit scheme for representing the letters A-Z.

Code for translating letters
So messages get broken up into 2-character blocks, because two 5-bit numbers concatenated give you a 10-bit block. This is most easily seen by an example:
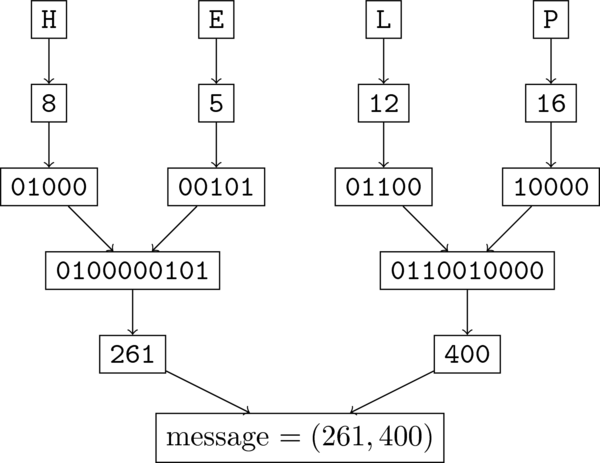
Message for "HELP"
So from our perspective, the "message" is (261,400). That's the thing we need to encrypt so it can't be understood by anyone who intercepts it during communication. Each of the two numbers will be encrypted separately, so the scheme extends to any length message.
5.2 Public Key Encryption
For most of human history, encryption meant "private key" encryption. If "Alice" was sending "Bob" information, they needed to agree on some kind of "key" ahead of time. In the digital age, however, we have to initiate secure communications with people with whom we've had no opportunity to exchange secret keys with. If you stumble across thinkgeek.com for the first time and decide to buy something, you suddenly need to communicate securely with someone completely new. This requires a new paradigm for encryption — "public key cryptography".
5.3 Introduction to the RSA
We'll be looking at the RSA algorithm, which is the "public key" cryptography system most commonly used today. The recipient has a "public key" consisting of two numbers \((e,n)\), and a "private key" consisting of two numbers \((d,n)\); note that n is the same in both. If you have a sequence of k bits comprising your message, where \(2^k \lt n\), you view those k bits as the binary representation of a number M with \(0 \le M \lt 2^k\). We encrypt the number M using the recipient's public key:
encrypt(M) = \(M^e \bmod n\) = E
To decrypt, the recipient uses his private key:
decrypt(E) = \(E^d \bmod n\) = M
The magic, of course, lies in how the numbers n, e, and d are chosen.
Example: Suppose Bob has public key \((e,n) = (37,8633)\) and private key \((d,n) = (685,8633)\). He makes the public key available to the whole world, but keeps his private key for himself only. Alice wants to send the message "HELP" (see the above) to Bob, which she does using his public key.
Alice sends (5096, 1385):
"HELP" \(\to\) (261, 400) \(\to\) \((261^e \bmod n, 400^e \bmod n)\) \(\to\) (5096, 1385)
Now Bob receives the message from Alice and decrypts it with his private key:
Bob receives "HELP":
(5096, 1385) \(\to\) \((5096^d\bmod n, 1385^d\bmod n)\) \(\to\) (261, 400) \(\to\) "HELP"
Notice: Alice was able to send Bob a message that (we hope!) only he can decrypt without any prior arrangement. In fact, anyone can create a message only Bob can decrypt, because everyone has access to his public key. This is pretty amazing, if you think about it.
Assuming we master the magic of choosing e, d and n, this looks great. However, as we'll discuss later, in order to ensure the security of this scheme, these need to be very large numbers ... on the order of \(2^{1000}\). Now aren't you glad we know how to do fast modular exponentiation?
5.4 RSA: Generating Keys
We need e, d, and n to satisfy the following equation for any message M: \((M^e)^d = M \bmod n\). This just means that the scheme actually works — that the decrypted message is the same as the original one. The left hand side simplifies to \(M^{ed}\), so we have a big power of M needs to equal M itself, mod n. Have you seen something like this before?
Yes! Remember \(3^{2013}\bmod 5\)? We figured out that this is just equal to 3 because \(\varphi(5)=4\) and 2013 mod 4 equals 1. So for RSA we want \(ed = 1 \bmod \varphi(n)\). Now the way the algorithm works, e needs to be chosen randomly. So we know e, and we need to figure out d. What can we do? Use the XGCD algorithm to compute the multiplicative inverse of e modulo \(\varphi(n)\).
But wait! What's \(\varphi(n)\)? Remember this is the number of integers less than n that don't share a common factor with n. But computing that's going to take a while in general. If we chose n to be a prime number, then it would be easy: \(\varphi(n)=n-1\). Unfortunately, this is too easy, because then anyone who knows the public key \((e,n)\) would be able to figure out the private key \((d,n)\) as well.
Instead, we'll choose \(n=pq\) where p and q are both (large) prime numbers. You can convince yourself (or just take my word for it) that in this case \(\varphi(n) = (p-1)(q-1)\). So if we construct n ourselves, then we know p and q and can compute \(\varphi(n)\). But anyone who just knows n can't compute p and q without factoring n. And as we saw before, no one knows any good algorithms to factor integers. So we can compute the private key \((d,n)\), but no one else can!
Putting this together, we have the following scheme for generating a public/private key pair for RSA:
- Assuming that we want to be able to encrypt k-bit messages, we generate two distinct random prime numbers p and q (i.e. \(p \ne q\)), each at least \(\frac{k}{2} + 1\) bits long, and set \(n = pq\).
- Choose e randomly such that \(2 \le e \lt (p-1)(q-1)\) and \(\gcd((p-1)(q-1),e) = 1\).
- Use the XGCD algorithm to compute d such that \(de = 1 \bmod (p-1)(q-1)\). More specifically:
- compute
XGCD((p-1)*(q-1), e), which gives us \((g,s,t)\). - if \(t\lt 0\) then \(d = t + (p-1)(q-1)\) else d = t.
- compute
Beginning of Class 16
6 Analysis of RSA
There are two things we should be dying to know:
- How long does it take to generate a public/private key pair?
- How long does it take to encrypt or decrypt a message with the proper keys?
- How long would it take to decrypt a message without the private key?
Naturally we want the encryption to be fast or people won't be able to send any messages!
More importantly, we want decryption with the private key to be much much faster than without it. And more than just a "tweak" (i.e. constant factor) faster — we want the growth rate of the decryption algorithm without the key to totally dominate the cost of legal decryption, so that the scheme stays useful even when computers get faster.
6.1 Primality Testing
The one part of the scheme that you don't really know how to do yet is the step in key generation where we need random prime numbers with a certain number of bits. How do we do such a thing?
Well, it turns out the prime numbers are relatively "dense" in the integers. That means, a lot of integers are prime, even big ones. Specifically, the proportion of k-bit integers that are prime is \(\Theta(1/k)\). So if we choose \(\Theta(k)\) random k-bit integers, there's an excellent chance at least one of them is going to be prime. (Yes, I've skipped over the details of the probabilistic analysis.)
But which one? What we need is a way of checking whether a given number n is a prime number. We could try and compute the factorization of n, but that's going to be REALLY slow (see above).
Now think back a few lectures ago — remember Fermat's Little Theorem? It implies that, if n is a prime number, then for any positive integer \(a \lt n\), \(a^{p-1} = 1 \bmod n\). In fact, prime numbers are the only ones that have this property for every possible a. This leads to an idea for primality testing: for a bunch of different a's, compute \(a^{p-1}\bmod n\), and if it's not 1 then we know n is not prime.
Unfortunately this doesn't quite work. (In particular, there is a whole class of numbers called the Carmichael numbers that will always trick such a test into thinking they are prime, even though they aren't.) But the following algorithm fixes this problem by dealing with factors of 2 dividing \(p-1\) specially, and it's the most commonly used primality test in practice:
Miller-Rabin Test
Input: Positive integer
nOutput:
Trueifnis prime, and otherwiseFalsewith high probability.def probably_prime(n): # This function returns a random integer from 2 up to n-2. a = random.randrange(2, n-1) d = n-1 k = 0 while d % 2 == 0: d = d // 2 k = k + 1 # IMPORTANT: This next line should be done more efficiently!! x = a**d % n # ** is the exponentiation operator if x**2 % n == 1: return True for r in range(1, k): x = x**2 % n if x == 1: return False if x == n-1: return True return False
Now notice that this is a probabilistic algorithm, meaning that sometimes it will return "PRIME" when n is really composite. However, the chance that this will happen is small, less than \(\frac{3}{4}\).
Not willing to gamble on 25%? Well how about this: repeat the Miller-Rabin test 41 times, and the probability that it incorrectly returns "PRIME" every time, but n is really composite, is much less than the chance that a cosmic ray from outer space will change your answer from "no" to "yes" anyway. (No, I am not making this up.)
I'll leave it to you to see that this algorithm runs in \(O(\log n)\) iterations, since the number of iterations of both loops is exactly the same, and is bounded by the number of times we can divide d by 2 before it is odd.
Actually, there is a "better" algorithm for primality testing, the famous "AKS" algorithm discovered in 2001, which is also polynomial-time in the size of n but is not randomized, and hence always returns the correct answer. However, the Miller-Rabin test is the fastest one and it is used most often in practice, and in particular in most implementations of the RSA algorithm that I know of.
6.2 Run-time analysis of playing by the rules
So what is the asymptotic cost of executing the RSA scheme (key generation, encryption with public key, decryption with private key)? It all basically comes down to three subroutines:
- Modular exponentiation, for example computing \(M^e \bmod n\). If we use the square-and-multiply algorithm this requires \(\Theta(\log e)\) multiplications mod n, each of which costs \(\Theta((\log n)^2)\) (as we'll see next unit). So the total cost is \(\Theta((\log e)(\log n)^2)\).
- Generating random primes with \(O(\log n)\) bits. Using Miller-Rabin, we might have to test \(\Theta(\log n)\) numbers before we find a prime one, and the algorithm requires \(\Theta(\log n)\) multiplications mod n, for a total worst-case cost of \(\Theta((\log n)^4)\).
- Running the XGCD algorithm to find multiplicative inverses. We already did this analysis; the cost is \(\Theta((\log n)^3)\).
The key to the security of RSA is the key length, which corresponds to the number of bits in the modulus n. Call this \(k\in\Theta(\log n)\). The worst-case cost of key generation is \(\Theta(k^4)\) and of encryption and decryption is \(\Theta(k^3)\). These are both polynomial-time, so even as the key lengths get longer and longer, computers will be able to handle these computations.
6.3 Security guarantees?
The security of RSA relies on a chain of assertions:
- The only way to decrypt a message is to have the private key \((d,n)\).
- The only way to get the private key is to first compute \(\varphi(n)\).
- The only way to compute \(\varphi(n)\) is to factor n.
- There is no algorithm for factoring a number that is the product of two large primes in polynomial-time.
Unfortunately, none of these assertions has been rigorously proved. But a whole lot of smart people have tried, and failed, for decades, to disprove them. So we're safe for now at least...
What this all means is that, as the key length k increases, the cost of factoring, and hence of decryption without the private key, will grow much much faster than the cost of "playing by the rules" above. This says that, no matter how much faster your computer is than mine, there is some key length for which the time it takes you (an attacker) to decrypt will be arbitrarily longer, say one million times longer, than the time it takes me (the good guy with the private key). This is what cryptography is all about!
By the way, in practice, these days, the recommended key-length for RSA is about 2000 bits or more.