1 Linear data structures

So far we have looked at essentially two data structures, linked lists and arrays. These are pretty powerful: they can implement a variety of different ADTs with some subtle and important differences between them, and they can do everything really quickly when you only add or remove things from the ends (as with stacks and queues).

We can call these data structures “linear” because they really form in a straight line, with a strict ordering from the first to last element that is stored. That can be good for efficiency when you only need to access the first and/or last thing in there, but accessing or modifying an arbitrary element is always going to be slow, \(O(n)\) time.

2 Trees

Trees are the first kind of data structure that frees us from this linear constraint. They are going to be exponentially more powerful (literally!) than linked lists and arrays, but also more difficult to maintain. Trees are also very visual and very fun to learn about; the data structures we will learn about here are true “classics” in the history of computer science.

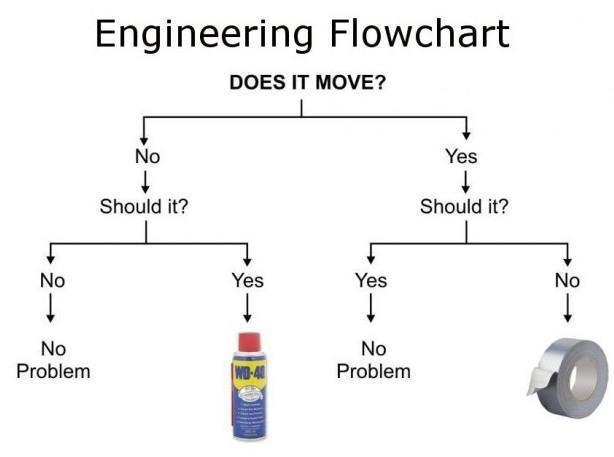
Let’s start with a simple example of a tree:

This is known as a decision tree. You see that a single node is at the top (“Does it move?”). This is the root. The root has two branches, to “No, should it?” and “Yes, should it?” Each of nodes also has two branches, one to “No/Yes, No problem,” and the other to “No/Yes, WD-40/Duct Tape.” Since every node in the tree has two branches, it’s called a binary tree.

More generally, we could give you the mathematical definition of a tree, but here is a recursive definition (of a rooted, binary tree):

A tree is either empty, or it contains a single root node connected to 0 or more trees below it.

We will initially focus on binary trees, where each node has at most 2 children. The decision tree above is a binary tree. Here is a more general example of a binary tree. Note that some nodes have 2 children, some have 1 child, and some have none.

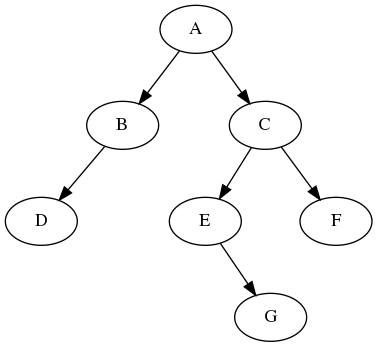
Here are some definitions of terms that we use to talk about trees. In parentheses are examples of each thing in the picture above.

• Node : an element of the tree (A, B, C, D, etc.)
• Root : The single element at the top of the tree (A)
• Parent : A node’s parent is the node immediately above it. Every node, except the root, has exactly one parent. (parent of E is C)
• Child : A node’s children are the nodes immediately below it. In a binary tree, every node as at most 2 children (children of A are B and C)
• Sibling : Two nodes are siblings if they have the same parent (E and F are siblings)
• Ancestor : Parent, or parent’s parent, or etc. (C is an ancestor of G. So are A and E.)
• Leaf : A node with no children (D, G, F)
• Internal Node : A node with at least one child. (A,B,C,E). Every node is either a leaf or internal node.
• Subtree : A portion of a tree that is, itself, a tree (recursion!). (For example, the subtree starting under node C has 4 nodes, C, E, F, and G.)
• Depth : The depth f a node is the number of edges that have to be traversed to encounter the root. (The depth of E is 2. The depth of A is 0.)
• Height : The most number of edges on any path from the root to a leaf. This is the same as the maximum depth of any node in the tree. (The tree above has height 3.) We will say that the height of an empty tree is -1.
• Branching Factor : The maximum number of children for a node is the branching factor. (It’s 2 for any binary tree.)

3 Implementing Trees

So what does this look like in Java? We’ll write this for a binary tree, or a tree where each node has up to two children.

public class Tree<T> {

  private class Node {
    public Node left  = null;
    public Node right = null;
    public T data;

    public Node(T d) {
      data=d;
    }
  }

  private Node root = null;

  // constructors, some other methods too...

One of the methods we might want is height() to get the height of the tree. As above, height is defined as the maximum depth of any node. To do that calculation, we should think recursively.

Consider that the height of the full tree is one bigger than the maximum of the heights of the two subtrees beneath the root where the root’s children are the root of the subtree. And then within each of those subtrees, it is the maximum of the heights of the two sub-subtrees, and so on.

This leaves us with a nice recursive method like so:

  public int height() {
    return heightFrom(root);
  }

  private int heightFrom(Node n) {
    if (n == null) return -1;

    int lh = heightFrom(n.left);
    int rh = heightFrom(n.right);

    return Math.max(lh, rh) + 1;
  }
}

Now, consider writing this same method iteratively. How might you do it? Well, we could use a Stack or Queue to do some tracking of heights to ensure we’ve traversed all the paths, but it will get ugly really quickly. Regardless, it will definitely NOT be 4 lines of code!

This is one of the many reasons that recursion is so important. It allows us to express fairly complex routines compactly and with clarity. So, if you are still struggling to understand recursion, be sure to ask questions because these examples will continue to come about.

4 Tree Traversals

Just like we needed to know how to traverse a Linked List, we need to know how to traverse a Tree. In a Linked List, the work we were doing to each Node could come either before or after the recursive call; this determined whether that work was done from the front of the list to the back, or from the back to the front. We have a similar concept here for trees, we just have more options.

4.1 Preorder Traversal

In preorder traversal, we have the rule that the node we’re looking at must be visited before its children; there are no rules as to the order of its children, or grandchildren. In the following code, I’m going to use process() in place of whatever work you’re doing to each node (maybe you’re printing each data point, or whatever). Preorder traversal looks like this:

preorder(Node n) {
  process(n.data);
  for( Node child : n) //for each child of n
    preorder(c);
}

4.2 Postorder Traversal

In postorder traversal, the node we’re looking at is visit after its children. It looks like this:

postorder(Node n) {
  for(Node child : n) //for each child of n
    postorder(cc);
  process(n.data);
}

4.3 Inorder Traversal

We’re going to deal with a lot of binary trees in this class. With a binary tree, we also have the option of Inorder Traversal, which is where you visit the left subtree first, then this node, then the right subtree

inorder(Node n) {
  inorder(n.left);
  process(n.data);
  inorder(n.right);
}

Here’s the same binary tree example from the beginning of the unit:

These traversals would visit the nodes in the following order:

• Preorder: A B D C E G F
• Inorder: D B A E G C F
• Postorder: D B G E F C A

Work carefully and make sure you follow this!

5 Level-order Traversal

Level order traversal is easy to do visually, but harder to do computationally. Unlike preorder and postorder traversals which are depth-first in nature (they descend all the way to the leaves of one subtree before moving on to the next), a level-order traversal is breadth-first. And in order to search in a breadth-first manner, we need a queue:

levelOrder() {

  //create a queue for the nodes
  nodesQueue = new Queue<Node>();
  nodesQueue.enqueue(root);

  while(nodesQueue.size() > 0){

    n = nodesQueue.dequeue();

    //reached a leaf, nothing to do
    if(n == null): continue

    //process current node and enqueue its children
    process(n.data);
    enqueue(n.left);
    enqueue(n.right);
  }

The level-order traversal of the example tree above would be A B C D E F G.

6 Binary Search Trees

We’ve learned a lot of things about trees, but we haven’t actually put any data in them yet. In a Binary Search Tree, we require that our data be sortable, and the rule is this: everything in the left subtree of a node is less than the node’s data, and everything in the right subtree is greater. Pretty simple, right?

Here’s some code to make that happen, if the tree is storing integers. The insert() method adds an element to the tree, and find() returns a boolean as to whether that element appears in the tree.

public class BST {
  private class Node {
    int key;
    Node left = null;
    Node right = null;

    public Node(int key) { this.key = key; }
  }

  private Node root = null;

  public void insert(int key) { root = insertUnder(root, key); }

  private Node insertUnder(Node uu, int key) {
    if (uu == null) // add a new leaf
      return new Node(key);

    if (key < uu.key) // smaller - go left
      uu.left = insertUnder(uu.left, key);
    else if (key > uu.key) // larger - go right
      uu.right = insertUnder(uu.right, key);
    // Notice no else case. If key == uu.key then there's nothing to do!
    return uu;
  }

  public boolean find(int key) { return findFrom(root, key); }

  private boolean findFrom(Node uu, int needle) {
    if (uu == null) // not found
      return false;
    else if (needle < uu.key) // smaller - go left
      return findFrom(uu.left, needle);
    else if (needle > uu.key) // larger - go right
      return findFrom(uu.right, needle);
    else // needle == uu.key
      return true;
  }
}

7 Deletion

Notice that when we add to a binary tree, we can always add a new leaf node. This makes life easier — if we needed to add somewhere in the middle of the tree, we would have to figure out how to rearrange the existing nodes and children to make that work, and it gets messy. So when adding to a binary tree, we always go all the way down to the bottom and make a new leaf node.

But when removing a node, we don’t have this luxury. We have three cases to consider when removing an node from a binary tree, depending on how many children the node that we want to remove has:

• 0 children (leaf node): easy. Just remove that one node! (In a good recursive method implementation, this means returning null.)
• 1 child (“elbow node”): easy. Replace that node with its one child.
• 2 children (“internal node”): hard. We can’t just remove or replace it, because there would be two children to take the place of one node…

OK, so let’s focus on the “hard” case, removing an internal node that has two children. Here’s the trick: we want to find another node which is “easy” to remove but which can replace the current node in terms of ordering. So swap these two nodes and then remove the “easy” one.

Specifically, we will swap the internal node with its successor, which is the next node in sequence within the tree. If the internal node we want to remove has two children, then its successor must be in the right subtree, and in fact it will be the smallest node in the right subtree.

This successor node has two important properties: First, it won’t mess up the ordering to replace the internal node we want to remove with its successor, since the successor will be larger than everything in the left subtree and smaller than everything else in the right subtree. Second, the successor node must be an “easy” case for removal because it can’t possibly have a left child. Why not? Well, if the successor had a left child, then it wouldn’t be the smallest node in that subtree!

In summary, here is how to handle the “hard” case of removing an internal node with two children:

1. Find the successor (smallest node in the right subtree).
2. Replace the current node’s value with the successor’s.
3. Remove the successor from the right subtree.

For example, starting with this tree:

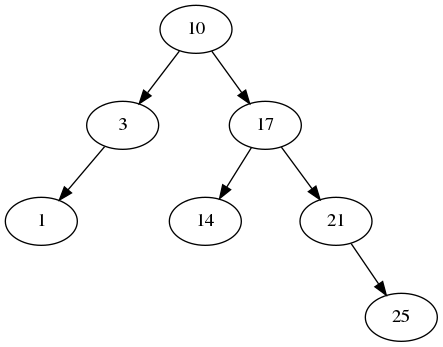
• Removing a leaf node like 1, 14, or 25 is easy — you just remove it (and the parent pointer).
• Removing a one-child “elbow” node like 3 or 21 is also pretty easy. You replace that node with the subtree of its only child.
• Removing a two-child “internal” node like 10 or 17 is hard. Taking 10 as an example, you would first find the successor of 10 in the right subtree — that’s 14 in this example. Then the 10 is replaced with 14, and finally 14 is (easily) removed from the right subtree. The picture below shows what the tree would look like after 10 is removed. Confirm for yourself that it’s still a binary search tree!

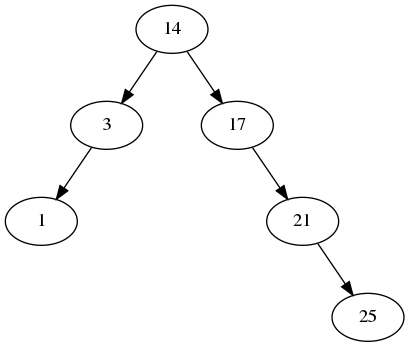
Here is a complete implementation of removal, continuing the BST class from above. Notice that we made two recursive helper functions: one to do removal, and one to find the successor value.

public void remove(int key) { root = removeUnder(root, key); }

private Node removeUnder(Node cur, int needle) {
  if (cur == null)
    throw new NoSuchElementException("could not find the needle to remove it");
  else if (needle < cur.key)
    cur.left = removeUnder(cur.left, needle);
  else if (needle > cur.key)
    cur.right = removeUnder(cur.right, needle);
  else { // found it!
    // first check easy cases
    if (cur.left == null)
      return cur.right;
    else if (cur.right == null)
      return cur.left;
    else {
      // hard case: cur.left and cur.right are both not null
      // find the successor and remove it
      int successor = getMin(cur.right);
      cur.key = successor;
      cur.right = removeUnder(cur.right, successor);
    }
  }
  return cur;
}

private int getMin(Node cur) {
  if (cur.left == null)
    return cur.key;
  else
    return getMin(cur.left);
}

8 Method Runtime

Traversal in a BST requires visiting every node, so that still costs \(O(n)\) time. But the other methods like find, insert, and remove have a worst-case running time proportional to the height of the tree, which could be much less than n.

How much smaller could the height be? Well, one way to answer this is to flip the question around and ask how many nodes could fit in a tree of height h. If you experiment a little bit, you should see that we get this two-sided inequality for the number of nodes in a height-h tree:

\[h+1 \le n \le 2^{h+1} - 1\]

Now you can solve each side for \(h\), to flip it around and get a two-sided inequality for how many nodes can be in a binary tree of a certain height:

\[\lg(n+1) - 1 \le h \le n-1\]

So we can’t say exactly what the height of a BST is, except to say that it is somewhere between \(O(log(n))\) and \(O(n)\), which is a massive range. For now we will just say the runtime of find, insert, and remove is \(O(h)\).