This is the archived website of IC 312 from the Fall 2022 semester. Feel free to browse around; you may also find more recent offerings at my teaching page.

Unit 3: ADTs and 1-D data structures

1 Abstract Data Types

Allegedly, this course is about Data Structures. In actuality, it is about Abstract Data Types (ADTs) and their implementation with Data Structures. An ADT is a description of an interface, and the data structures are how we make them work. For instance, last semester, we built a Queue. A Queue is an ADT; the linked list is the data structure.

2 Two implementation issues

As we have said, this is not a class in Java programming. But there are two issues we have to look at before we can even talk about how an ADT is realized in Java.

These issues aren’t actually unique to Java, but are common to just about every programming language with some notion of objects, and different languages have slightly different ways of handling it.

2.1 Generic Storage

One important thing to consider with ADT’s is that they do not specify what kind (or type) of element they can store. This creates a challenge when our language (like C++ or Java) wants us to declare types for everything!

To understand the issue, consider defining a class for a linked list of strings in Java:

public class LinkedListOfString {
    private class Node{
      String data;
      Node next;
    }

    Node head = null;

    int size() {/*---*/}
    String get(int i) {/*---*/}
    void set(int i, String e) {/*---*/}
    void add(int i, String e) {/*---*/}
    String remove(int i) {/*---*/}
}

This implementation is fine and well whenever we want to store Strings, but what if we want to store ints or doubles or Objects or whatever we want? We have to copy paste the code and create a whole new implementation at each of the types. That, is simply, a nightmare for a programmer.

What we want is to write one implementation of the data structure that can store all the things we want. One way to do this is to leverage the subclassing in Java and recognize that Object is the base type, and, thus, everything is a subclass of Object. Maybe we could define our LinkedList implementation like so:

public class LinkedListOfObject {
    private class Node{
      Object data;
      Node next;
    }

    Node head = null;

    int size() {/*---*/}
    Object get(int i) {/*---*/}
    void set(int i, Object e) {/*---*/}
    void add(int i, Object e) {/*---*/}
    Object remove(int i) {/*---*/}
}

Now when we use this implementation, we have to cast the elements going in and going out of the data structure as the implementation expects and returns Objects, not the specific type we are using. For example, this code will produce a compiler error:

LinkedListOfObject lst = new LinkedListOfObject();

lst.add(0, "Bob");
lst.add(1, "Barker");

if (lst.get(0).charAt(0) == lst.get(1).charAt(0)) {
  System.out.println("Both first letters are the same.");
}

The calls to lst.add() are actually OK here — Java automatically upcasts the strings like "Go" to type Object because String is a subclass of Object.

But the last line will cause a compiler error, because lst.get() returns an Object rather than a String like we added.

Take a moment to ponder this. We have a situation where we, the programmers, know that everything in the list is a String, but the compiler doesn’t. To solve it, we have to explicitly downcast every time we call get(), like

if (((String)lst.get(0)).charAt(0) == ((String)lst.get(1)).charAt(0)) //...

This is not only very annoying and verbose, but it’s also error-prone because the checks are only performed at runtime instead of compile-time. If we used the wrong type for the downcast, it would never be noticed until execution actually hits that line of code.

And the calls to add, which work above because the compiler will upcast automatically, are also error-prone with no type checking at compile time. For example, we could write

lst.add(1, 17); // 17 is not a String!

and nothing would go wrong until we try to do (String)lst.get(1) and Java realizes — at runtime — that 17 is not a String.

Generics in Java are the way around this. They allow us programmers to communicate to the compiler that we know all the types in the data structure will be the same thing, but that they can be anything. And the compiler will do the type checks and casting at compile-time, saving us from writing casts all the time and (more importantly) from having bugs that don’t get noticed until later.

To use generics, you define the type for the class in angle brackets (<>), and this acts as a “meta-argument” to the constructor defining the type that is being stored. Using generics, we get the definition of the LinkedList from the homework:

public class LinkedList<T> {
    private class Node{
      T data;
      Node next;
    }

    Node head = null;

    int size() {/*---*/}
    T get(int i) {/*---*/}
    void set(int i, T e) {/*---*/}
    void add(int i, T e) {/*---*/}
    T remove(int i) {/*---*/}
}

Notice that we’ve specified a new type-variable, T, that defines what type of elements the LinkedList stores. It doesn’t have to be called T, but the convention is to always use a single upper-case letter.

2.2 Iterators and Lists

To motivate iterators, consider the following simple code for iterating over a List lst.

for(int i=0; i<lst.size(); i++) {
  lst.get(i);
}

What is the runtime of this procedure? First consider the ArrayList or FixedList implementation which uses an underlying array storage. It’s, \(O(n)\), right? The get() operation requires a constant number of operations to access the array at index i and return the element, and we call get() n times.

What if we are using the recursive LinkedList implementation? To get() an element we must traverse from the head of the list to index i. Since each call to get() is \(O(n)\), and we call it n times, the total cost is \(O(n^2)\).

Frankly, that sucks. This should clearly be \(O(n)\). How do we get there?

The problem with the iteration above for linked list is that it doesn’t preserve any state when you are doing the iteration. Every get() requires you to start over! That’s where the additional \(n\) factor comes in and you get \(O(n^2)\) instead of \(O(n)\).

Java provides a means to overcome this issue using an Iterator, and you can find the documentation here. The Iterators interface has just two required methods (where E is the generic):

//return true if the iteration has more elements
boolean hasNext();

//Returns the next element in the iteration
E next();

What this interface enables is that a new Iterator is generated at the start of each interaction, storing where in the iteration we are at. You can keep calling next() until there are no more elements, and you can check the case where we’ve reached the end using hasNext().

We won’t spend too much time implementing Iterators in this class, but just to show you how this all fits together, here’s an Iterator implementation for the recursive LinkedList:

import java.lang.Iterable;
import java.util.Iterator;

//now implements Iterable
public class LinkedList<T> implements Iterable<T> {

  private class Node{
    T data;
    Node next;
  }

  Node head = null;

  int size() {/*---*/}
  T get(int i) {/*---*/}
  void set(int i, T e) {/*---*/}
  void add(int i, T e) {/*---*/}
  T remove(int i) {/*---*/}

  // Iterable interfaces require that you can return an Iterator
  @Override
  public Iterator<T> iterator(){
      return new LLIteartor(head);
  }

  // the Iterator we will return
  private class LLIterator implements Iterator<T> {
    private Node cur;

    public LLIterator(Node start) { cur = start; }

    public boolean hasNext() { return cur != null; }

    public T next() {
      T data = cur.data;
      cur = cur.next;
      return data;
    }

    // this is part of the java.util.Iterator interface but optional
    public void remove() { throw new UnsupportedOperationException();}
  }
}

Now, we can use the LinkedList in a foreach iteration like so:

LinkedList<String> lst = new LinkedList<>();
lst.add(0, "Go Navy!");
lst.add(1, "Beat Army!");

//foreach iteration, assign s to each element in lst using the Iterator methods
for(String s : lst) {
  System.out.println(s); //prints "Go Navy!", then "Beat Army!"
}

3 The List ADT

We’ve been using the List ADT in our homework assignments, and so far you’ve seen two different implementations of a List: the FixedList and the recursive LinkedList. To review, here are the following methods that must be defined for a List

get(i): return the data at the i-th place in the list.
set(i,e): return the i-th piece of data, and also replace it with e.
add(i,e): insert e in the list at location i. All data with locations greater than i are shifted to a location one greater.
remove(i): remove and return the data at i. Shift all data at higher indices down.
size() return the number of elements in the list.

This is all an ADT is! Any way of making this work, no matter how stupid or slow, still means that it is a list. However, implementing it with different data structures gives us different run times, and thus the choice of implementation can have a big impact on the performance of your program. Perhaps you should use an array back end, like FixedList or ArrayList, or a linked node structure like LinkedList. Presumably, you could implement all four of those methods with a combination of strategies.

3.1 The size() method for List

You can pretty easily imagine how size() is implemented for an array-based list — you just get the length of the array. But for a linked list, we have been iterating over the whole list and counting, taking \(O(n)\), right?

Well, all that work could be easily avoided by storing one extra little piece of data in the Linked List class; namely, an int for the current size of the list. This value would be updated on each add() or remove() operation, and returned by each a call to size().

public class LinkedList<T> implements List<T>, Iterable<T> {
    private class Node {
        T data;
        Node next;
    }

    Node head = null;
    int length = 0;

    public int size() { return length; }

    public void add(int i, T e) {
        /* modify the actual list ... */
        length += 1;
    }

    public T remove(int i) {
        /* modify the actual list... */
        length -= 1;
    }

    public T get(int i) {/*---*/}
    public void set(int i, T e) {/*---*/}
    public Iterator<T> iterator() {/*...*/}
}

There is something subtle but important about why this is okay: An ADT implementation is allowed to store extra data besides whatever information the ADT itself specifies.

In the case of a List, the ADT just specifies that you are storing an ordered sequence of elements. It says nothing about storing the size. But your data structure is allowed to store the size, in order to make the <code>size()</code> operation more efficient! The key is actually that the total storage is still the same in terms of big-O, since \(n+1 \in O(n)\).

3.2 Big-O of Lists, so far

After all of that work, we can now chart the big-O of our list implementations:

	ArrayList	LinkedList
get()	\(O(1)\)	\(O(n)\)
set()	\(O(1)\)	\(O(n)\)
add()	\(O(n)\)	\(O(n)\)
remove()	\(O(n)\)	\(O(n)\)
size()	\(O(1)\)	\(O(1)\)
iteration	\(O(n)\)	\(O(n)\)

4 Amortizing The Cost of ArrayLists Expansion

Given the previous discussion on lists, it is hard to remember where the advantages of Linked Lists comes from, but there are advantages. Particularly, Linked Lists are much better when adding to the ends of the list, either the front or the back because it only requires reassigning the pointers.

With linked lists, regardless if you are inserting at the front or the end, this is \(O(1)\). Array Lists, however, are \(O(n)\).

This fact may not be obvious at first, but consider that if you were to insert at the beginning of the list, which corresponds to index 0 in the underlying storage array, to make space for that element requires shifting the other \(n\) elements to the right. That’s \(O(n)\).

You might think that inserting at the end of the list would improve things, and, if there is space in the storage array, that operation will be constant time. But, that doesn’t tell the whole story and is the best case scenario. What about the worst case scenario? What if the storage array is full?

If the storage array is full, then you’ve got to make more space. The only way to do that is to create a new and larger array and then copy all the elements into the new array, including the new value to add. The copying of all the elements, that’s \(O(n)\).

So, in both special cases, inserting at the front or back of an Array List is going to be \(O(n)\). It would seem, if you are in such circumstances, the Linked List reigns supreme. However, this doesn’t paint the full picture. It is possible to make adding to the end of an array-based list significantly faster.

4.1 Doubling Array Storage on Expansion

First, suppose we had an infinitely-sized array. Adding to the front would still be \(O(n)\), because all \(n\) items would have to be shifted to make room at index 0. Adding at the end, however, would be \(O(1)\), because there’s an empty space there!

Obviously, an infinitely-sized array is impossible. However, let’s use the scheme that every time we run out of room on our array, we double the size of the array. Will we have lots of unused indices? Yup. But, if our biggest number of elements in the list is \(n\), the most memory we’ll use is \(2n\). And, while that might hurt, at least that’s still \(O(n)\). (Yup! We can and do use Big-O in reference to memory, too!)

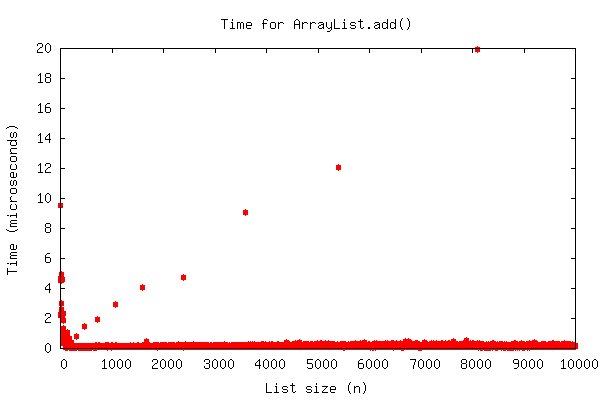
Now, we only resize every time we actually fill this too-big array. Isn’t the worst case still \(O(n)\)? Well, sort of. For the first time, our “number of operations as a function of \(n\)” function isn’t smoothly increasing; instead, it’s spiky. This is because almost all of the time, adding to the end is O(1) because there will be space for the new element. However, every now and then, it’s O(n). See:

If you drew a line threw those little red “outlier” dots, it’d be a straight line; \(O(n)\). But almost all the dots are right there at the bottom, \(O(1)\), not increasing at all even with thousands of elements in the array.

The question is, on average, are there enough \(O(1)\) operations to make up for the occasional \(O(n)\) operation? In other words, is it true that regardless of the size of the array, on average, the time required does not change?

The answer, actually, is yes, and what lets us say this is amortized analysis.

4.2 Amortized Analysis

Pretend you have a business. Every 10 years, you have to buy a 100,000 dollar machine. You have two ways you could consider this; either, every ten years you lose massively, having to pay all 100,000, or every year you put aside 10,000 to be used later. This is called amortizing the cost. We can do the same thing here.

Let’s assume assigning one element to an array is 1 operation. Again, if we double the size of the array every time we need more space, starting with an array of size one, we would get the following series of costs when adding 17 elements to an initially-empty array: 1 2 3 1 5 1 1 1 9 1 1 1 1 1 1 1 17.

The reason is that when the size reaches \(1, 2, 3, 5, 9, 17\), which is 1 more than each power of 2, we have to allocate a new array and copy everything over. So those are the “outlier” and expensive additions. But all the other additions are cheap; they just involve copying a single element.

But we can amortize these expensive additions over the previous “cheap” ones! Check it out:

Size	`1`	`2`	`3`	`5`	`9`	`17`
Actual	`1`	`1 2`	`1 2 3`	`1 2 3 1 5`	`1 2 3 1 5 1 1 1 9`	`1 2 3 1 5 1 1 1 9 1 1 1 1 1 1 1 17`
Amortize	`1`	`3 0`	`3 3 0`	`3 3 3 3 0`	`3 3 3 3 3 3 3 3 0`	`3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 0`

Noticing the theme? No matter how big our list becomes, the amortized cost of a single add never gets bigger than 3. So, the cost of an add, even with resizing the array, is \(O(1)\) (amortized). In other words, the size of the \(O(n)\) operations is increasing at the same rate as the number of \(O(1)\) operations to smooth it out over.

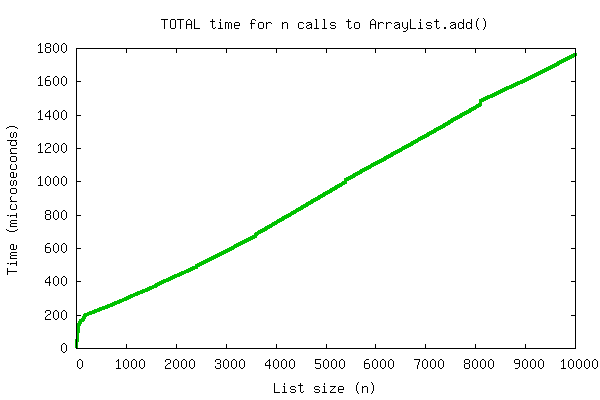
Another way of putting this is that the sum total cost of a series of \(n\) additions onto the end of an initially-empty array is \(O(n)\). In fact, if we take the same graph as above and plot the running sum instead of the individual cost of each operation, the fact that this line is \(O(n)\) becomes fairly obvious:

If doing an operation \(n\) times requires a total of \(O(n)\) work, then each individual operation must be \(O(1)\).

As you may already know, this is in fact exactly how Java’s ArrayList class works. Using similar ideas they can also remove from the end of an ArrayList in \(O(1)\) amortized time, and guarantee that the space usage is kept at \(O(n)\). In fact, the previous graphs came from timing Java’s own ArrayList!

There is one additional problem with the doubling-size array implementation of a List: the size of the array no longer matches the size of the list! So just like with linked lists, we have to store an extra int for the “actual” size of the list, which will always be less than the size of the array. Again, this keeps the storage as \(O(n)\) and so it’s okay.

What if we don’t double the size of the array on expansion?

It is very important for amortized analysis that the storage array doubles when it is full (or, at least, that it increases by a multiplicative factor - tripling its size, for example, would be fine, too), rather than just having a constant number of empty spaces added on, otherwise the analysis from before falls apart. The add-to-back operation becomes \(O(n)\) again. To see this we must use a bit of notation to express the amortized concepts from above. First, lets show, again, that the amortized cost of add-to-back for an array list that expands by doubling is \(O(1)\). Using that baseline, we can show that if we do something less than doubling, say constant size expansion, we go back to being an \(O(n)\) operation.

4.3 Showing that add-to-back is O(1) amortized for doubling

Let’s do the analysis of doubling the array on expansion, but this time with a bit more math. To start, we can define a term \(c_i\) that is the cost of the i-th insertion to the end of the list. This would be the formula for the “Actual” row in the table from above (where a non-expanding insert only costs one step).

\[ c_i = \begin{cases} i & \text{if } \ \ (i-1) \ \ \text{is a power of 2}\\ 1 & otherwise\\ \end{cases} \]

In the above definition, it costs either constant time, 1 step, or i steps to do the insertion. It costs i steps when (i-1) is a power of 2, which is when we do expansions. What we must now show to demonstrate \(O(1)\) amortized cost is that total costs of \(n\) insertions should be \(O(n)\) for add-to-back insertion, and thus each individual insertion costs \(O(1)\) amortized. That’s the same argument we made above, and mathematically we can write the summation.

\[ \sum_{i=1}^{n} c_i = n-\lfloor lg(n) \rfloor + \sum_{j=0}^{ \lfloor lg(n) \rfloor } (2^j + 1) \]

Solving the summation we recognize that there is \(n - \lfloor lg(n) \rfloor\) operations that cost a constant amount of time, where we are subtracting the number of times we need to expand the array, \(\lfloor lg(n) \rfloor = \lfloor log_2(n) \rfloor\). The next item to solve for is the cost of all the expansions. Since we expand on powers of 2 and we do so \(\lfloor lg(n) \rfloor\) times, the cost of the number of expansions is solving the following summation.

\[\begin{array}1 ∑~j=0~^\ ⌊\ lg(n)\ ⌋\ ^ 2^j^ + 1 &= ∑~j=0~^\ ⌊\ lg(n)\ ⌋\ ^ 2^j^ + ∑~j=0~^\ ⌊\ lg(n)\ ⌋\ ^ 1\ &= ∑~j=0~^\ ⌊\ lg(n)\ ⌋\ ^ 2^j^ + ⌊ lg(n) ⌋ &= 2n - 1 + ⌊ lg(n) ⌋ \end{array}\]

Fortunately, the solution involves the geometric sum, whose solution is as follows.

\[ \sum_{i=0}^{n-1} r^i = \frac{1-r^n}{1-r} \]

Substituting in 2 for \(r\), we get that \(\sum_{j=0}^{ \lfloor lg(n) \rfloor } 2^j = 2n-1\). And, we now have everything to complete the analysis.

\[ \sum_{i=1}^{n} c_i = n-\lfloor lg(n) \rfloor + 2n - 1 + \lfloor lg(n) \rfloor = 3n - 1 \]

This says it costs \(O(n)\) to insert \(n\) items to the end of the list, thus each insertion costs \(O(1)\) amortized.

4.4 Showing that add-to-back is O(n) amortized with constant size expansion

Let’s do the same analysis again, but this time instead of doubling the list, we expand by a constant factor. For example, we start with a list of size \(k\) and once the array is full, we will expand it to size \(2k\), and then to \(3k\), and so on. In that scenario, we define \(c_i\), the cost of each insert like so:

\[ c_i = \begin{cases} i & \text{if } \ \ (i-1) \ \text{ mod } \ k = 0\\ 1 & otherwise\\ \end{cases} \]

The cost of insert is O(n) at each factor of \(k\) because that is when the array is full and must be copied into a new array. If we consider the costs of \(n\) insertions to the end of the list, we can again solve the summation, but it looks a bit different now.

\[ \sum_{i=1}^{n} c_i = n - \lfloor n/k \rfloor + \sum_{j=0}^{\lfloor n/k \rfloor} (k \cdot j +1) \]

From this summation, it is clear that there are many constant operations, but there are now many more non-constant operations \(\lfloor n/k \rfloor > \lfloor lg(n) \rfloor\) as expansion occurs on each factor of \(k\) rather than each power of 2. Further, looking at the costs of the expansions, for the total number of times we expand, it costs \(k \cdot j+1\) where \(j\) is the count of the number of expansion. We know how to solve the sum for the cost of all the summation as it is just a sum of a sequence of numbers:

\[ \sum_{j=0}^{\lfloor n/k \rfloor} (k \cdot j+1) = \lfloor n/k \rfloor+k \cdot \sum_{j=0}^{\lfloor n/k \rfloor} j = \lfloor n/k \rfloor+k \cdot \left ( \frac{\lfloor n/k \rfloor (\lfloor n/k \rfloor + 1)}{2} \right) = \lfloor n/k \rfloor+\frac{k}{2}({\lfloor n/k \rfloor}^2 + \lfloor n/k \rfloor) \]

Substituting that back into the other formula, we get this result for the cost of \(n\) insertions.

\[ \sum_{i=1}^{n} c_i = n + \frac{k}{2}({\lfloor n/k \rfloor}^2 + \lfloor n/k \rfloor) \]

If you look closely, you see the \({\lfloor n/k \rfloor}^2\) term dominates, which makes this \(O(n^2\)) to insert \(n\) items to the end of the list with constant expansion. Thus it is \(O(n)\) amortized to insert each item, and that is no good.

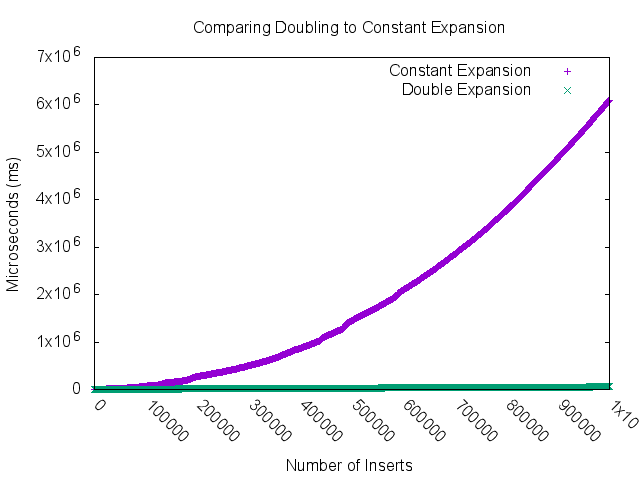
Finally, you can also see this fact clearly if were to measure the speed of two routines, one using doubling expansion and one using constant expansion.

Clearly, the constant expansion is increasing faster than the doubling expanding line, and precisely, one is \(O(n^2)\) and the other \(O(n)\). The moral of the story is that you have to (at least) double the size of the array when expanding otherwise you do not get \(O(1)\) amortized costs of expansion.

5 Stack ADT

Our second ADT is the Stack. We’re pretty familiar with Stacks already, so this might not be so hard. Stacks work like a stack of plates: you only add plates onto the top of the stack, and you only remove stacks from the top of the stack. This makes them a LIFO (last-in-first-out).

The methods of a stack are:

push(e): Add element e to the top of the stack.
pop():Take the top element off the top of the stack, and return it.
peek() : Return the top element of the stack, without altering the stack.
size() : Return the number of elements in the stack

Let’s consider an example. On the left column of this table, I will have some commands. In the middle, I’ll put what is returned, if anything. On the right, I’ll put the state of the stack, with the top of the stack on the left.

Command	Returned Value	Stack
		empty
`push(3)`	-	`3`
`push(5)`	-	`5 3`
`pop()`	`5`	`3`
`peek()`	`3`	`3`
`push(4)`	-	`4 3`
`peek()`	`4`	`4 3`
`pop()`	`4`	`3`
`pop()`	`3`	empty

5.1 Stack Implementations

Implementation with Linked Lists should seem relatively easy to you; if “first” refers to the top element of the stack, then push() is just an add-to-front, pop() is a remove-from-front, and peek is just return first.getData(); (modulo error checking for an empty stack, of course).

This means that for stacks implemented by linked lists, all three methods can be run in \(O(1)\) time. Great!

What about arrays? Well, if we used a “dumb” array, each push() and pop() would cost \(O(n)\) because of the need to copy the entire contents each time. But as we saw above with amortized ArrayList, we can be smart about this and leave some empty space in the array, doubling it when necessary. You could technically also shrink the array (halving when necessary) in pop(), but that makes everything more cumbersome, so we’ll assume the resizings only happen during push() only.

	LinkedList	ArrayList
`push()`	\(O(1)\)	\(O(1)\) amortized
`pop()`	\(O(1)\)	\(O(1)\)
`peek()`	\(O(1)\)	\(O(1)\)

5.2 Usefulness of Stacks

OK, so stacks are fast! What can we do with them?

Reverse stuff - pushing everything on, and then popping it all off puts it in reverse order.
Maze solving - every time you come to a junction, push it on the stack. When your decision doesn’t work out, pop to the last junction, and go the other way. If there are no more possible directions, pop again.
For more complex uses of stacks, stay tuned…

And, you’ll see Maze solving in the project!

6 Queue ADT

We know Queues well from IC211. If a Stack is a LIFO (Last-In First-Out), then a Queue is a FIFO (First-In First-Out). In other words, things come out in exactly the same order they went in.

Think about a line for the checkout counter at the grocery store (after all, “queue” is British for “line”). People can only join the line at the end, and only leave the line at the front. In between, they never switch order.

The methods a Queue must have are:

enqueue(e): Add an element to the back of the Queue
dequeue(): Remove and return the front element of the Queue
peek(): Return, but do not remove, the front element of the Queue
size(): Return the number of elements in the queue

6.1 Implementing a Queue with a Linked List

Implementation with a Linked List is fairly straightforward. Enqueue is just an add-to-back operation, which is \(O(1)\) if we have a tail reference to track the last Node in the linked list. Just like we discussed with the size() operation, adding new book keeping elements is totally fine for a ADT.

Dequeue is also simple, and is remove-from-front operation, which, again, is \(O(1)\). We already track the front of the list with a head reference, so we are good to go there.

Finally, peek() is the same as dequeue() but without removal. That operation just returns the value of the first Node in the list, like head.getData(), which is clearly \(O(1)\).

So, Linked Lists are great(!) at implementing Queues. What about arrays?

6.2 Implementing a Queue with Array Storage

6.3 Challenges of using an array for Queues

The challenge of using array storage to implement a Queue is hindered by have to tracking the first element in the queue. There are two obvious choices for this, the front of the queue could either be index 0 or the list or the size-1 of the list (or the last element in the list).

If we were to use index 0 as the head of the queue, then enqueue is simply an add-to-back operation which we know is \(O(1)\) amortized. But what about dequeue? When we dequeue an element, we are performing a remove-from-front operation, and that requires shifting the remaining elements towards the front. For a naive array implementation, that could be \(O(n)\), and that’s bad.

We come up against a similar problem if we were to use size-1 as the front of the queue. In that case dequeue is \(O(1)\) since you are removing from the end of the list, but enqueue is now an add-to-front operation, which requires shifting all the elements to the right in the storage array. The shifting operation is \(O(n)\).

So, it would seem that arrays simply are no good for implementing queues. Like with stacks, though, we can get fancy and still get constant time operations.

6.4 Circular Arrays

One way to solve this is with what we’ll call a Circular Array. In the circular version, you track the number of elements in the list (size) and the current first index (head). For example:

public class CircularArrayList<T> implements List<T> {

 private int head=0;
 private T elements[];

 //..
}

The difference between an ArrayList and a CircularArrayList is that the start index of an ArrayList doesn’t change, but it may in a CircularArrayList. And, in particular, the head of the CircularArrayList changes in a remove-from-front operation.

  |
  v
.---------------------------.     size()=4
| 0 | 1 | 2 | 3 |   |   |   |     head=0
'---------------------------'

remove(0) or dequeue()

      |
      v
.---------------------------.     size()=3
|   | 1 | 2 | 3 |   |   |   |     head=1
'---------------------------'

remove(0) or dequeue()

          |
          v
.---------------------------.     size()=2
|   |   | 2 | 3 |   |   |   |     head=2
'---------------------------'

Enqueue, or the add-to-back operation, becomes a bit more complicated because we need to calculate the end of the list. It is no longer just at array[size] as it was in the ArrayList implementation. But, it’s easy to calculate as array[head+size], and we can perform any add()’s there and continue to well track the list.

add(size(),4); or enqueue(4)

          |
          v
.---------------------------.     size()=3
|   |   | 2 | 3 | 4 |   |   |     head=2
'---------------------------'


add(size(),5) or enqueue(5)

          |
          v
.---------------------------.     size()=4
|   |   | 2 | 3 | 4 | 5 |   |     head=2
'---------------------------'

add(size(),6) or enqueue(6)

          |
          v
.---------------------------.     size()=5
|   |   | 2 | 3 | 4 | 5 | 6 |     head=2
'---------------------------'

The next issue we need to consider is, what happens when we’ve reached the end of the array? Well, there may be more free slots in the front of the array if the head > 0. What we want to do is wrap-around, and it’s easy to do that calculation using a modulo to determine the end of the list array[(head+size())%array.length] (or any requested index in the list, where size is replaced by i, the index being requested).

In the end, after one more enqueue() / add() in the example above, we have the following array layout.

add(size(),7) or enqueue(7)

          |
          v
.---------------------------.     size()=6
| 7 |   | 2 | 3 | 4 | 5 | 6 |     head=2
'---------------------------'

This wrapping around is why we call it a circular array list because, over time with adds and removes, the front and end of the list circle back around on each other.

The last implementation detail to consider is the resizing: What happens when the array is completely full? Fortunately, this is the same as expanding the storage array for an ArrayList, and we know that this cost can be amortized over all the add() operations. (If you want to, when you resize, you could even rearrange the array such that head becomes 0 again).

Now, it should be clear to you that an add-to-front and a remove-from-back for a Queue implemented with an array is \(O(1)\) amortized and \(O(1)\), respectively.

	LinkedList	Array
`enqueue()`	\(O(1)\)	\(O(1)\) amortized
`dequeue()`	\(O(1)\)	\(O(1)\)
`peek()`	\(O(1)\)	\(O(1)\)

IC 312 Fall 2022 / Notes

What if we don’t double the size of the array on expansion?