The problems with parse trees

The starter code for today’s class is a “beefed-up” calculator language that includes things like assignment and comparison. Here’s the grammar (bison style):

run: stmt run
|    stmt

stmt: ares STOP

ares: VAR ASN bres
|     bres

bres: res
|     bres BOP res

res: exp
|    res COMP exp

exp: exp OPA term
|    term

term: term OPM factor
|     factor

factor: NUM
|       LP bres RP
|       VAR

And here’s a simple program in this language:

x := (5 + 3) * 2;
x > 3 - 7;

Now check out the parse tree for that “simple” program:

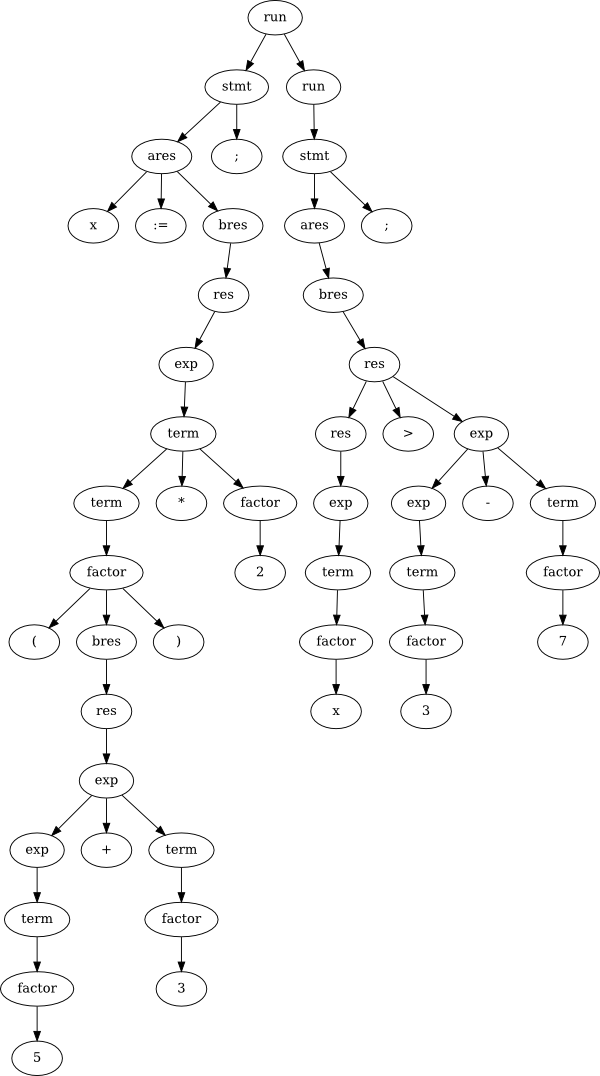
That’s pretty messy and huge! We will see in lab how the grammar can be simplified somewhat to help shrink down the waste, but that only goes so far. As you know from implementing some simple interpreters in your lab, all this complication in the grammar directly affects the speed of interpreting (or compiling) programs in the language. When programs get really big, and we want to compile them really quickly, this becomes an issue.

An even more critical issue can arise when the syntax of our grammar doesn’t match the desired semantics of the language. For example, the natural way to make an operator be left-associative is to write the grammar using left recursion. But, as you know, left recursion doesn’t work with top-down parsers. So we rewrite the grammar to be right-recursive (using all those tail rules). This makes the parsing go faster, and is fine if you are writing the parser and interpreter together (like in your recursive descent parser lab). But if the program gets more complicated, we will notice quickly that the parse tree that results from this top-down grammar with tail rules is essentially right-associative rather than left. In other words, the parse tree (syntax) doesn’t match the semantic meaning of the program. What can we do about this?

1 Abstract Syntax Trees (ASTs)

Abstract Syntax Trees (ASTs) provide a way of representing the semantic meaning of our program in a simple way that is independent of the actual syntax. This is a little confusing, so I’ll emphasize again that the AST has nothing to do with the syntax - it’s an abstraction away from the syntax of the language!

Unlike with a parse tree, which is uniquely defined according to the grammar (as long as the grammar is not ambiguous), there isn’t just one definition of exactly how the AST for a particular program should look. Think of the AST as a useful internal representation for the interpreter or compiler, which may be slightly different depending on the language or capabilities of the implementation.

In this class we will try to be fairly consistent in how we draw ASTs and what they mean. Every node in the AST is either a statement or an expression. We’ve already discussed in previous units how these are different from each other; basically an expression is any self-contained program fragment which has a type and evaluates to some value, whereas a statement is a self-contained program fragment which does something, but doesn’t return any value. A while loop or a function definition are good examples of statements, and a variable name or arithmetic operation are good examples of expressions.

Here’s an example of an AST for the same example from before (just putting the two statements inside curly braces so they form a single Block statement):

{
    x := (5 + 3) * 2;
    x > 3 - 7;
}

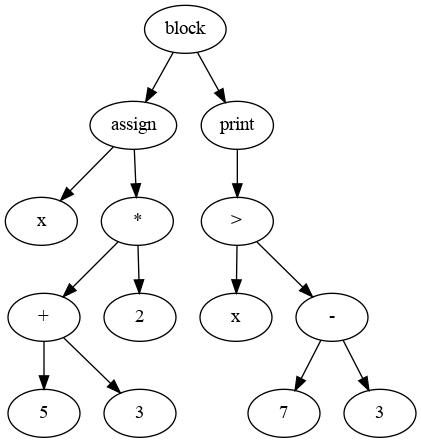
The first thing you should notice is that this is a lot simpler than the previous parse tree. This AST represents the actual meaning of our small program - what that program is actually supposed to do.

Notice how the arithmetic operations like times and greater-than are represented. The operation goes up top (or any function call, for that matter), and the arguments go below it, in order.

The top three nodes (block, assign, print) are a bit different - they are statements rather than expressions. These statements are ordered, and that ordering is expressed by the order of the children of the “block” node. Unlike almost any other AST node, a block can have any number of children, and each of those child nodes will be the individual statements inside the block.

You should also observe that this AST is simpler in most respects than the preceding parse tree, but it also has some new things that the parse tree didn’t. For example, in the program above, it’s implicit that an expression should be printed out if it’s not part of an assignment. The AST makes this explicit.

One more thing to make sure you notice: the AST does not depend on a single programming language. For example, I bet you could write the Scheme program or the C++ program corresponding to the AST above pretty easily. Moreover, a Scheme program that does exactly the same thing could generate exactly the same AST as a program in another language! Of course, the specific components of some language will affect what’s in the AST (for example, no lambdas in our calculator language), but the point is that the AST doesn’t depend on any syntactical choices of the language - only on the meaning of the program.

2 Static type checking

Assume booleans are a “real” type in your language (i.e., they’re not just integers like in C), and you have a program like (7 > 2) + 3. This is an error because 7 > 2 is a boolean, and you can’t add a boolean to a number. Specifically, it’s a type error, because the problem is that the types of the two operands for the plus operator are “incompatible”, meaning basically that they can’t be added together.

When we talk about compilation, a lot of things are divided between “static” or “dynamic”. This sometimes means different things in different context, but usually it’s:

• Static means something is computed or known at compile-time, before actually executing the program.
• Dynamic means something is computed or known only at run-time, as the program executes.

Generally speaking, the more we can do statically (at compile-time), the better. The reasoning behind this is that you only need to compile your program once, and afterwards it can of course be executed many, many times.

Here we’re specifically talking about catching type errors, and this is always a nice thing to do at compile-time if we can. Why? Well, maybe this type error is buried somewhere deep in the user’s code. Maybe the program does some big, long, difficult computation, and then at the very end, just as it’s about to display the brilliant result, it gets a type error and crashes. What a tragedy! If we had compile-time (static) type checking, that wouldn’t happen, because that error would have been noticed by the compiler before the program ever started running.

The AST is created at compile-time, just after the parsing phase. So any type-checking we do with the AST will be static-time checking. For a simple expression like (7 > 2) + 3, the process is pretty simple: starting at the leaves, we label every node in the AST with its type. Whenever there’s an operation like > or +, we check that the types of the arguments are compatible, and then label the node with the type of whatever results. In this case, the > node gets labeled as a boolean, and of course 3 is a number, so when we go to label the + node, we see that these are incompatible and give an error.

More specifically, static type checking is performed by labeling all AST nodes which are expression with their types, and checking in all non-leaf nodes that the types of sub-expressions are compatible. What is meant by “compatible” will be different for different nodes: for example, a multiplication node may require that both sub-expressions are numeric types, whereas an if statement node may require that its condition is a boolean.

Hooray! Errors are a good thing - they save the programmer time and help assure that the actual program (with no errors) works as intended. But static type checking gets a lot more complicated when we have variables. Look back up at the AST for this program above:

x := (5 + 3) * 2;
x > 3 - 7;

To do the type-checking here, we would need to know the type of x in the second statement, in order to check that it’s actually a number and therefore compatible with 3 - 7 in the > operation. Of course you can wee that, yes, x is going to be a number here. But how would the compiler know? In order to do this kind of type checking, we would need static typing, which means that the types of every variable are known at compile-time. For example, Java has static typing; that’s why you have to declare the types of all your variables!

Scheme, on the other hand, is not statically typed. In fact, it would be impossible to do static type-checking in Scheme. Consider the following example program:

(define a (if (read) 'symbol 15))
(+ a 20)

This is a perfectly valid Scheme program, which reads in something from standard in, assigns variable a accordingly, and then tries to add that to 20. But it’s impossible to know the type of the variable a at compile-time, and therefore impossible to know without running the program whether (+ a 20) will result in a type error. In short, the flexibility of a language like Scheme which doesn’t make us declare the types of variables has a dark side, which is that we have to wait until run-time to discover errors or bugs in our code. Would you want to fly in a plane controlled by a Scheme program?

But before we can really talk about static typing, we have to answer the more fundamental question of what does a variable refer to, at any given point in the program. This means we need to know about things like scope. Which is what the next unit’s all about!