Remember to turn in a neat final draft of this homework on a separate sheet of paper.

AVL Tree Problems

1. Draw the tree that would result after performing a left rotation at node 13 of the following tree:
   
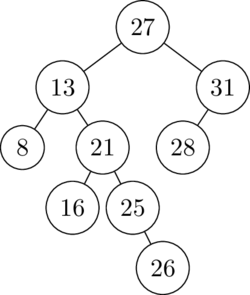
2. Copy the following tree and write in the balance factors at every node. Then perform any rotation(s) to make it an AVL tree and show the result.
   

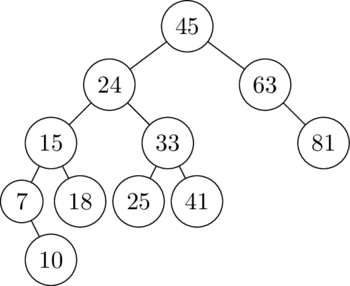
For the next two problems, start with an empty AVL tree and insert each of the given nodes, in the order given. Rebalance the AVL tree after every insertion. You do not need to draw every single step separately, but you must draw the tree immediately before every rotation, and say what the rotations are.

3. 29, 9, 12, 89, 17, 84
4. 77, 82, 2, 25, 54, 27, 21, 95, 65

2-3-4 Tree Problems

For the next two problems, starting with an empty 2-3-4 tree, insert each of the given letters into the tree, in the order given. Show your work, and clearly indicate the final state of the 2-3-4 tree after all the insertions.

5. F L A M E T H R O W I N G
6. L U M B E R J A C K

For the next two problems, I mostly need the final answer, but you need to show your work That might mean showing the series of trees that you made to find the answer, or explaining how else you figured it out. Of course, you should clearly indicate your final answer.

7. Starting with an empty 2-3-4 tree, and inserting the letters of the alphabet A, B, C, D, ... in order, the first time the tree would grow to height 1 would be after inserting D.
   After inserting what letter would the tree grow to height 2 for the first time?
8. Now answer the same question, but for height 3. So, starting with an empty tree and inserting A, B, C, ... in order, after inserting what letter would the tree grow to height 3 for the first time?
9. BONUS PROBLEM: Come up with an exact formula for the maximum number of nodes in a 2-3-4 tree of any height \(h\), if insertions are performed the way we did it in class.